Cinemática
Matemáticas: Trigonometría, derivadas, integrales.
- Cinemática: Movimiento en una dimensión.
- Movimiento rectilíneo uniforme: la velocidad constante.
- Movimiento uniformemente acelerado: la caída libre.
- Tiro parabólico (movimiento en dos y tres dimensiones).
- Resistencia del aire. Cuando la aceleración no es constante.
La cinemática
La cinemática es una rama de la mecánica clásica que estudia el movimiento de los cuerpos sin tomar en consideración las causas que lo producen.
Para estudiar el movimiento primero tenemos que entender dos conceptos básicos, posición y tiempo, con los que se busca describir el estado de un sistema en todo momento. Se comienza por establecer un sistema de referencia y elegir un sistema de coordenadas, a partir de los cuales la posición de un objeto en una, dos o tres dimensiones se define como el desplazamiento a lo largo de cada una de las direcciones del sistema de coordenadas elegido desde el punto de referencia establecido.
La posición es un conjunto de cantidades escalares (números reales) que nos permiten determinar el lugar que ocupa un cuerpo u objeto en un espacio de coordenadas espaciales (1D: línea; 2D: plano; 3D: espacio tridimensional; ND...). En mecánica se considera que estas cantidades tienen unidades de desplazamiento espacial y dependiendo del sistema de coordenadas que utilicemos este puede tratarse por ejemplo de desplazamientos lineales o angulares.
El objetivo de la cinemática consiste en describir la
El reposo: la posición constante
En términos de cinemática, la situación más simple en la que podemos pensar es aquella en la que la posición de un cuerpo no cambia, es decir que permanece constante al pasar el tiempo. A esta situación tan particular se le conoce como
Entonces la trayectoria en una dimensión de una partícula en reposo que al tiempo de referencia \(t=t_0\) se encuentra en la posición \(x=x_0\) estará dada simplemente por \(x(t)=x_0\) donde \(x_0\) es una constante. (Quizás aquí un estudiante podría pasar al pizarrón a dibujar esta trayectoria). \[ x(t)=x_0=cte. \]
\begin{tikzpicture}[domain=0:8,range=0:20] \begin{axis}[title=\textbf{El reposo}, xmax=8,% xmin=0,% ymax=20,% ymin=0,% height=9cm, width=0.95\textwidth, grid=major, xlabel=tiempo (segundos), ylabel=distancia (m) ] % use TeX as calculator: % Computer angle: %\def\col{10*\vel}% % \edef\col{0} % \pgfmathparse{\vel*10.0} % \edef\col{\pgfmathresult} \addplot[line width=3pt,color={blue!10!red}, mark=none] {10}; \node[fill=cyan] at (2cm,5cm) {$x_0=\unit{10}{\metre}$}; \end{axis} \end{tikzpicture}Esta situación es un caso particular (\(v=0\) del problema que analizaremos a continuación.
Movimiento rectilíneo uniforme: la velocidad constante
Cuando un cuerpo no se encuentra en reposo, para describir el estado de movimiento es necesario conocer también qué tanto cambia la posición conforme avanza el tiempo, es decir, se necesita conocer el ritmo de cambio de la posición en el tiempo. La cantidad física que se utiliza para esto es la que conocemos con el nombre de
Introducción a la utilización de las herramientas del cálculo diferencial e integral en la física: velocidad promedio y velocidad instantánea. \[ \bar{v}=\frac{\Delta x}{\Delta t} \] \[ v=\lim_{\Delta t\to 0}\frac{\Delta x}{\Delta t}=\frac{dx}{dt} \] \[ v=\frac{\mathrm{d}x}{\mathrm{d}t} \]
Discutir: unidades de la velocidad.
Supongamos ahora que tenemos un cuerpo que se mueve con velocidad constante, digamos \(v_0\), distinta de cero. ¿Cómo podemos extraer la trayectoria de la partícula únicamente a partir de esta información? De acuerdo con lo que acabamos de ver, \[ v=\frac{\mathrm{d}x}{\mathrm{d}t} \] Entonces, la pregunta que hemos planteado nos dice que \(v=v_0\), lo cual es equivalente a: \[ \frac{\mathrm{d}x}{\mathrm{d}t}=v_0=\mathrm{cte} \] Esto es una ecuación diferencial y tal como las igualdades y desigualdades estudiadas en álgebra, esta herramienta matemática establece una relación o regla que deben cumplir una serie de parámetros y variables, pero en este caso involucra además a los cambios (derivadas) de las variables mismas. Ahora, así como la suma y la resta o la multiplicación y la división, la derivada y la integral son operaciones complementarias y opuestas. Por lo tanto, para encontrar la ecuación de la trayectoria para el cuerpo que se desplaza a velocidad constante a continuación lo que tenemos que hacer es integrar a ambos lados la ecuación anterior: \[ \int \mathrm{d}x=\int v_0 \mathrm{d}t \] De este modo tenemos que la trayectoria del cuerpo que se desplaza con velocidad constante está dada por \eqref{EQ:VelCte1}: \begin{equation}\label{EQ:VelCte1} x(t)=v_0 t+C_0 \end{equation}
Discusión:
- ¿Qué tipo de gráfica representa esta ecuación?
- ¿Qué significado físico tiene la constante de integración \(C_0\)? Quizás convenga reescribir las integrales incluyendo los límites de integración. Poner énfasis en que cada término que aparece en una expresión matemática tiene que tener un significado físico. \begin{align*} \int^{x(t)}_{x_0} \mathrm{d}x &= \int_{t_0}^{t} v_0 \mathrm{d}t' \\ x\Big|_{x_0}^{x(t)} &= v_0 t'\Big|_{t_0}^{t} \\ x(t)-x_0 &= v_0(t-t_0) \end{align*} Por lo tanto: \begin{equation}\label{EQ:VelCte2} x(t) = x_0 +v_0(t-t_0) \end{equation} donde desde los límites de integración se ha establecido que \(x_0\) corresponde a la posición del cuerpo al tiempo \(t=t_0\).
- Hacer gráficas de velocidad como función del tiempo y de posición como función del tiempo en las que se observe el significado de las operaciones de derivación e integración.
Ejercicio: velocidad promedio
Un corredor recorre una pista de \( \SI[per-mode=fraction]{200}{\metre} \) en \(\unit{25}{\second}\). ¿Cuál es (a) la rapidez promedio y (b) la velocidad promedio del corredor?
- La rapidez promedio será la distancia neta recorrida entre el tiempo que le toma recorrerla: \[ \bar{v}=\frac{\Delta x}{\Delta t}=\frac{\unit{200}{\metre}}{\unit{25}{\second}}=\unit{8.0}{\metre \, \second^{-1}} \]
- Dado que el recorrido comenzó y terminó en el mismo punto, el vector de desplazamiento tiene longitud zero: \[ |\bar{\vec{v}}|=\frac{\unit{0}{\metre}}{\unit{25}{\second}}=\unit{0}{\metre \, \second^{-1}} \]
Movimiento uniformemente acelerado: la caída libre.
Aceleración: ritmo de cambio de la velocidad como función del tiempo.
Discutir: las unidades de la aceleración.
Aceleración promedio e instantánea. Una vez más el cálculo. \[ \bar{a}=\frac{\Delta v}{\Delta t} \] \[ a=\lim_{\Delta t\to 0}\frac{\Delta v}{\Delta t}=\frac{\mathrm{d}v}{\mathrm{d}t} \] \[ a=\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\mathrm{d}x}{\mathrm{d}t}\right)=\frac{\mathrm{d}^2x}{\mathrm{d}t^2} \]
Veamos ahora qué pasa cuando tenemos un cuerpo que se desplaza con aceleración constante \(a_0\). \[ \frac{\mathrm{d}^2x}{\mathrm{d}t^2}=a_0 \] Una vez más nos encontramos con una ecuación diferencial que tenemos que resolver.
A continuación se realiza prácticamente el mismo proceso que se siguió en la sección anterior y quizás convenga involucrar a uno o más estudiantes para que realicen los pasos del cálculo, deduzcan la ecuación de movimiento, interpreten las constantes de integración, den un significado físico claro a cada uno de los términos de las ecuaciones de posición y velocidad, dibujen las gráficas en pizarrón, etc... \[ \frac{\mathrm{d}v}{\mathrm{d}t}=a_0 \] \[ \int \mathrm{d}v=\int a_0 \mathrm{d}t \] \[ v(t)=a_0 t + C_0 \] \[ v(t=0) = C_0 = v_0 \] \begin{equation}\label{EQ:vela0uno} v(t)=a_0 t + v_0 \end{equation} \[ \frac{\mathrm{d}x}{\mathrm{d}t}=a_0 t + v_0 \] \[ \int \mathrm{d}x=\int a_0 t \mathrm{d}t + \int v_0 \mathrm{d}t \] \[ x(t) = \frac{1}{2}a_0 t^2+v_0 t +C_1 \] \[ x(t=0) = C_1 = x_0 \] Por lo tanto, \begin{equation}\label{EQ:posa0uno} x(t) =x_0 + v_0 t + \frac{1}{2}a_0 t^2 \end{equation}
Ahora con los límites en la integral: \[ \frac{\mathrm{d}v}{\mathrm{d}t}=a_0 \] \[ \int_{v_0}^{v(t)} \mathrm{d}v'=\int_{t_0}^{t} a_0 \mathrm{d}t' \] \[ \left(v(t) -v_0\right)=a_0 (t-t_0) \]
Así se llega a la ecuación para velocidad en todo tiempo \(v\left(t\right)\) de un objeto en el movimiento uniformemente acelerado y que al tiempo \(t_0\) tiene velocidad \(v_0\): \begin{equation}\label{EQ:vela0dos} v(t) = v_0 + a_0 (t-t_0) \end{equation}
\begin{tikzpicture}[domain=4:8] \begin{axis}[height=9cm, width=0.95\textwidth, grid=major, xlabel=tiempo ($\second$), ylabel=velocidad ($\metre \, \second^{-1}$) ] % use TeX as calculator: \def\vel{2}% \foreach \acel in {0,...,5}{ % Computer angle: %\def\col{10*\vel}% \edef\col{0} \pgfmathparse{\vel*10.0} \edef\col{\pgfmathresult} \addplot[color={blue!100 !red}, mark=none] {\vel + \acel*(x - 4)}; } \node[fill=cyan] at (1cm,3cm) {$t_0=\unit{4}{\second}$}; \node[fill=cyan] at (1cm,4cm) {$x_0=\unit{10}{\metre}$}; \node[fill=cyan] at (1cm,5cm) {$v_0=\unit{2}{\metre \, \second^{-1}}$}; \node[fill=cyan] at (1cm,6cm) {$a_0=\unit{0,...,5}{\metre \, \second^{-2}}$}; \node[fill=Plum!20!White] at (7cm,6cm) {$v(t) = v_0 + a_0 (t-t_0) $}; \end{axis} \end{tikzpicture} \begin{align*} \frac{\mathrm{d}x}{\mathrm{d}t} &= v_0 + a_0 (t-t_0) \\ \int_{x_0}^{x} \mathrm{d}x' &= \int_{t_0}^{t} v_0 \mathrm{d}t' + \int_{t_0}^{t} a_0 (t-t_0) \mathrm{d}t' \\ \left(x(t)-x_0\right) & = v_0 (t-t_0) + \int_{t_0}^{t} a_0 t \mathrm{d}t' -\int_{t_0}^{t} a_0 t_0 \mathrm{d}t' \\ &= v_0 (t-t_0) + \frac{1}{2} a_0 t^2 \Big|_{t_0}^{t} -a_0 t_0 (t-t_0) \\ &= v_0 (t-t_0) + \frac{1}{2} a_0 t^2 -\frac{1}{2} a_0 t_0^2 -a_0 t_0 t + a_0 t_0^2 \\ &= v_0 (t-t_0) + \frac{1}{2} a_0 t^2 +\frac{1}{2} a_0 t_0^2 -a_0 t_0 t \\ &= v_0 (t-t_0) + \frac{1}{2} a_0\left( t^2 - 2 t_0 t + t_0^2\right) \\ &= v_0 (t-t_0) + \frac{1}{2} a_0 (t-t_0)^2 \end{align*}Finalmente, se llega a la ecuación para el movimiento uniformemente acelerado de un objeto cuya posición a todo tiempo es \(x\left(t\right)\) y que al tiempo \(t_0\) está en la posición \(x_0\) con velocidad \(v_0\): \begin{equation}\label{EQ:posa0dos} x(t) = x_0 + v_0 (t-t_0) + \frac{1}{2} a_0 (t-t_0)^2 \end{equation}
\begin{tikzpicture}[domain=4:8] \begin{axis}[title=\textbf{Aceleración constante}, height=9cm, width=0.95\textwidth, grid=major, xlabel=tiempo ($\second $), ylabel=disancia ($\metre $) ] % use TeX as calculator: \def\vel{2}% \foreach \acel in {0,...,5}{ % Computer angle: %\def\col{10*\vel}% \edef\col{0} \pgfmathparse{\vel*10.0} \edef\col{\pgfmathresult} \addplot[color={blue!10 !red}, mark=none] {10 + \vel*(x - 4) + 0.5*\acel*(x - 4)^2}; } \node[fill=cyan] at (1cm,3cm) {$t_0=\unit{4}{\second}$}; \node[fill=cyan] at (1cm,4cm) {$x_0=\unit{10}{\metre}$}; \node[fill=cyan] at (1cm,5cm) {$v_0=\unit{2}{\metre \, \second^{-1}}$}; \node[fill=cyan] at (1cm,6cm) {$a_0=\unit{0,...,5}{\metre \, \second^{-2}}$}; \node[fill=Plum!20!White] at (7cm,6cm) {$x(t) = x_0 + v_0 (t-t_0) + \frac{1}{2} a_0 (t-t_0)^2 $}; % \end{axis} \end{tikzpicture} La serie de Taylor: expansión en series de potencias \begin{align*} f(x)&=f(a)+\frac{f^\prime(a)}{1!}(x-a)+\frac{f^{\prime\prime}(a)}{2!}(x-a)^2+\frac{f^{\prime\prime\prime}(a)}{3!}(x-a)^3+\dots \\ &=\sum_{n=0}^{\infty}\frac{f^{(n)}(a)}{n!}(x-a)^n \end{align*}
Combinando las dos ecuaciones de movimiento \ref{EQ:posa0dos} y \ref{EQ:vela0dos} que acabamos de encontrar, podemos deducir una tercera que resulta útil en la solución de algunos problemas. Para esto tomamos la ecuación de la velocidad \ref{EQ:vela0dos} y la elevamos al cuadrado: \[ v^2=v_0^2+a_0^2 (t-t_0)^2 + 2 v_0 a_0 (t-t_0) \] \[ 2 v_0 a_0 (t-t_0)= v^2 - v_0^2 - a_0^2 (t-t_0)^2 \] A continuación, multiplicamos por $2a_0$ a la segunda ecuación \ref{EQ:posa0dos} \[ 2 a_0 (x-x_0) = 2 a_0 v_0 (t-t_0) + a_0^2 (t-t_0)^2 \] Ahora despejamos $2 v_0 a_0 (t-t_0)$ de ambas ecuaciones e igualamos los resultados \[ 2 a_0 (x-x_0) - a_0^2 (t-t_0)^2 = v^2 - v_0^2 - a_0^2 (t-t_0)^2 \] para llegar a que \begin{equation}\label{EQ:vela0tres} v^2=v_0^2+2 a_0(x-x_0) \end{equation}
De este modo podemos expresar el desplazamiento realizado a un tiempo dado \(t\) como función únicamente de la velocidad inicial, de la velocidad al tiempo en cuestión \(t\) y de la aceleración \(a_0\): \begin{equation}\label{EQ:deltax0tres} \Delta x(t)=(x(t)-x_0)=\frac{v(t)^2-v_0^2}{2 a_0} \end{equation}
Dinámica
El trabajo y la energía
El trabajo
El trabajo se define como la cantidad escalar dada por: \begin{equation} W=\int \vec{F}\cdot \mathrm{d}\vec{r} \end{equation} Recuérdese que el producto punto es la proyección de un vector sobre otro. Por lo tanto, el trabajo es igual a la integral de la proyección de la fuerza aplicada \(\vec{F}\) a lo largo de la trayectoria \(\vec{r}\) descrita por el cuerpo sobre el que actúa la fuerza.
El trabajo tiene unidades de fuerza por distancia: \[ \left[W\right]=\left[\vec{F}\cdot \mathrm{d}\vec{r}\right]=\mathrm{N}\cdot \mathrm{m}=\mathrm{Joule} \] El Joule es la unidad de "energía" del sistema internacional, pero ¿qué es la energía?
Regresa al inicioLa energía
La energía es un concepto abstracto que surge de la observación de que existe una cantidad física que en un sistema cerrado se conserva.
La energía es una medida de las acciones que se ejercen sobre un sistema dado y esta cantidad obedece una ley universal de conservación. La energía no se crea ni se destruye, únicamente se transforma de una forma a otra.
Regresa al inicioTeorema del trabajo y la energía
El trabajo expresa la habilidad de una fuerza de ejercer un cambio en la energía de un cuerpo o sistema. Considere una partícula de masa \(m\) que se mueve bajo la influencia de una fuerza neta constante, \( \vec{F}=\mathrm{cte} \) ( i.e. \( \vec{a}=\mathrm{cte.} \) ).
Si la partícula se desplaza una distancia \( d=(x_f-x_i) \) en la dirección de la fuerza, \begin{align*} \Rightarrow W&=\int\limits_{x_i}^{x_f} \vec{F}\cdot \mathrm{d}\vec{x} =F \int\limits_{x_i}^{x_f} \mathrm{d}x = F x \Big|_{x_i}^{x_f}= F(x_f-x_i)\\ &=F\times d=(m a) d \end{align*} donde \( F \) y \(a\) son respectivamente las magnitudes de la fuerza y de la aceleración. Ahora recordando nuestros conceptos de cinemática podemos escribir \[ d=\frac{1}{2}(v_i+v_f) t \] \[ a=\frac{(v_f-v_i)}{t} \] con \(v_i=v(t=0)\) y \(v_f=v(t)\) como las velocidades instantáneas al momento cuando se inicia el desplazamiento \(d\) y al tiempo \(t\) cuando se ha realizado el desplazamiento. Sustituyendo en la fórmula del trabajo \[ W=m\left(\frac{v_f-v_i}{t}\right) \frac{1}{2}\left(v_f-v_i\right) t \\ =\frac{1}{2}m\left(v_f-v_i\right) \left(v_f+v_i\right) \] \[ \Rightarrow W=\frac{1}{2}m v_f^2-\frac{1}{2}m v_i^2 \] Observe que en efecto cada uno de los dos términos de la expresión anterior tienen unidades de trabajo: \[ \left[ \frac{1}{2}m v^2 \right]= \mathrm{kg} \left(\mathrm{m/s}\right)^2= \left(\mathrm{kg\, m/s^2}\right)\, m=\mathrm{N\, m}=\mathrm{Joule} \]
Además, cada uno de los dos términos de la expresión dependen únicamente del estado de movimiento de la partícula en el momento inicial y final del desplazamiento. Por lo tanto, cada uno de estos términos pueden identificarse como la energía asociada el estado de movimiento de la partícula antes y después de aplicada la fuerza, por lo que el trabajo realizado puede ser identificado como el cambio de la energía de la partícula. Esto es, podemos definir a la energía cinética de una partícua de masa \(m\) que se mueve a una velocidad \(v\) de la siguiente manera: \begin{equation} K=\frac{1}{2}m v^2 \end{equation} De esta forma, el teorema de trabajo-energía resulta de relacionar al trabajo realizado por la fuerza con el cambio en la energía cinética: \[ W=K_f-K_i=\Delta K \]
Este mismo procedimiento lo podemos repetir aún si la fuerza no es constante: \[ W=\int\limits_{x_i}^{x_f}F_x\cdot \mathrm{d}x=\int\limits_{x_i}^{x_f}m a_x\cdot \mathrm{d}x \] Utilizando la regla de la cadena \( a_x=\frac{\mathrm{d}v}{\mathrm{d}t}=\frac{\mathrm{d}v}{\mathrm{d}x}\frac{\mathrm{d}x}{\mathrm{d}t}=v\frac{\mathrm{d}v}{\mathrm{d}x} \) \[ \Rightarrow \hspace{1cm} W=\int\limits_{x_i}^{x_f}m v\frac{\mathrm{d}v}{\mathrm{d}x}\cdot \mathrm{d}x=\int\limits_{v_i}^{v_f}m v \,\mathrm{d}v \] \[ \therefore \hspace{1cm} W=\frac{1}{2}m v_f^2-\frac{1}{2}m v_i^2 \]
Regresa al inicioLa energía potencial
La energía potencial es energía almacenada en un sistema que puede realizar trabajo o transformarse en energía cinética. La energía potencial la podemos asociar a fuerzas conservativas para las que la energía cinética ganada ó perdida por un sistema conforme sus constituyentes cambian sus posiciones relativas es balanceada por una pérdida o ganancia igual en energía potencial. Esto da lugar al principio de conservación de la energía mecánica.
Hagamos un ejercicio simple. ¿Cuál es la energía potencial de un cuerpo de masa \(m \) que se encuentra a una altura \(h\) con respecto al piso? Para resolver este problema calculemos la cantidad de trabajo que realizaría el campo de fuerza gravitacional sobre el cuerpo cuando este se deja caer desde la altura \(h\) y llega hasta el suelo. \[ W=\int\limits_{h}^{0}\vec{F}\cdot \mathrm{d}y=(-mg) y\Big|_{h}^{0}=(-mg)(0-h)=mgh \] Si ahora definimos a $U_g$ como la energía potencial gravitacional de modo que \(U_g=0\) en el suelo (\(y=0\), entonces necesariamente a una altura \(y=h\) tendremos que \[ U_g(y=h)=mgh \] Por lo tanto, el cambio en la energía potencial sufrido por el cuerpo en su desplazamiento entre la altura \(h\) y el suelo está dado por: \[ \Delta U_g=U_g(y=0)-U_g(y=h)=0-mgh=-mgh \]
Podemos ahora extender este mismo concepto para dos alturas arbitrarias y calcular el trabajo requerido para mover al objeto desde una posición inicial hasta una final: \[ W_g=-(U_f-U_i)=-\Delta U_g \] Esto quiere decir que el trabajo realizado sobre un cuerpo por la fuerza gravitacional es igual al negativo del cambio en la energía potencial gravitacional del sistema.
En general, el trabajo realizado por una fuerza conservativa es igual al negativo cambio de la energía potencial generada por la fuerza en el espacio. \begin{equation} W=-\Delta U \end{equation}
Problemas de trabajo y energía
- ¿Cuánto trabajo se realiza en contra de la gravedad al levantar un objeto de \(3\) kg a lo largo de una distancia vertical de \(40\) cm?
-
¿Cuánto trabajo realiza sobre un objeto una fuerza que lo sostiene mientras el objeto es descendido a través de una distancia vertical \(h\)? ¿Cuánto trabajo realiza la fuerza de gravitación en este objeto al realizar el mismo proceso?
Solución: El trabajo realizado por quien sostiene el objeto mientras desciende: \[ W_{f}=\int\limits_{h}^{0}\vec{F}\cdot \mathrm{d}y = F \int\limits_{h}^{0} \mathrm{d}y= (mg) y \Big|_{h}^{0}=(mg)(0-h) = -mgh \] Por otro lado, como se vió anteriormente, el trabajo realizado por la fuerza de gravedad es: \[ W_G=\int\limits_{h}^{0}\vec{F}\cdot \mathrm{d}y = F \int\limits_{h}^{0} \mathrm{d}y = (-mg) y\Big|_{h}^{0} = (-mg)(0-h) = mgh \]
- Calcule el trabajo realizado en contra de la gravedad por una bomba que descarga \(600\) litros de combustible en un tanque que se encuentra \(20\) m por encima de la toma de la bomba. \( 1\) cm\(^3\) de combustible tiene una masa de \(0.82\) g. \(1\) lt es igual a \(1000\) cm\(^3\).
- Una masa de \(2\) kg cae \(400\) cm. (a) ¿Cuánto trabajo ha realizado sobre esta masa la fuerza gravitacional? (b) ¿Cuánta energía potencial gravitacional ha perdido esta masa?
- Un bloque de \(0.5\) kg se desliza sobre la superficie de una mesa con una velocidad inicial de \(20\) cm/s y alcanza el reposo en una distancia de \(70\) cm. Encuentre la fuerza de fricción promedio que frenó este movimiento.
Solución: Este problema se puede resolver utilizando únicamente argumentos de trabajo y energía. Para empezar, el trabajo realizado por la fuerza de fricción es: \[ W= \int\limits_{x_i}^{x_f} \vec{F} \cdot \mathrm{d}\vec{x} = F \int\limits_{x_i}^{x_f} \mathrm{d}x =F(x_f-x_i)= F\, d \] Esto debido a que la magnitud \(F\) de la fuerza de fricción cinética es constante y su dirección es siempre paralela pero con sentido contrario al desplazamiento. A la vez, el teorema de trabajo y energía indica que este trabajo debe de ser igual al cambio en la energía cinética: \[ W = \Delta K = \frac{1}{2} m v_f^2-\frac{1}{2} m v_i^2 = - \frac{1}{2} m v_i^2 \] Por lo tanto, la fuerza de fricción es: \[ F = - \frac{m v_i^2}{2 d} \] Si resolvemos esto utilizando el procedimiento desarrollado en la sección de cinemática tendríamos posiblemente que: \[ a = \frac{v_f^2-v_i^2}{2 d} = -\frac{v_i^2}{2 d} \] Luego, por la 2a ley de Newton tenemos que \[ F= m a = -\frac{m v_i^2}{2 d} \] que es el mismo resultado al que llegamos antes.
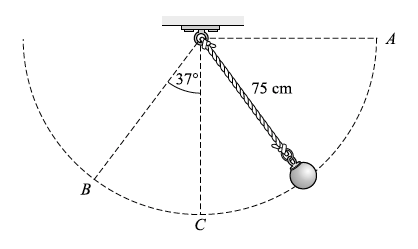
- Considere el péndulo simple mostrado en la figura. (a) Si la bola es liberada desde el punto A, ¿cuál será la velocidad de la bola cuando esta pase a través del punto C? (b) ¿Cuál es la velocidad de la bola en el punto B?
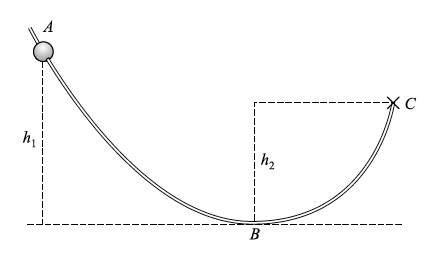
- La figura muestra una cuenta resbalando en un alambre. ¿Qué tan grande debe de ser la altura \( h_1 \) para que la cuenta, iniciando desde el reposo en el punto A, alcance una velocidad de \( 200\) cm/s en el punto B?
- Suponga que \(h_1=50\) cm, \(h_2= 30\) cm, la longitud a lo largo del alambre desde A hasta C es de \(400\) cm, y una cuenta de \(3\) g liberada desde A alcanza el punto C donde se detiene. ¿Qué tan grande es la fuerza de fricción promedio que se opone a este movimiento?
El péndulo simple (energía)
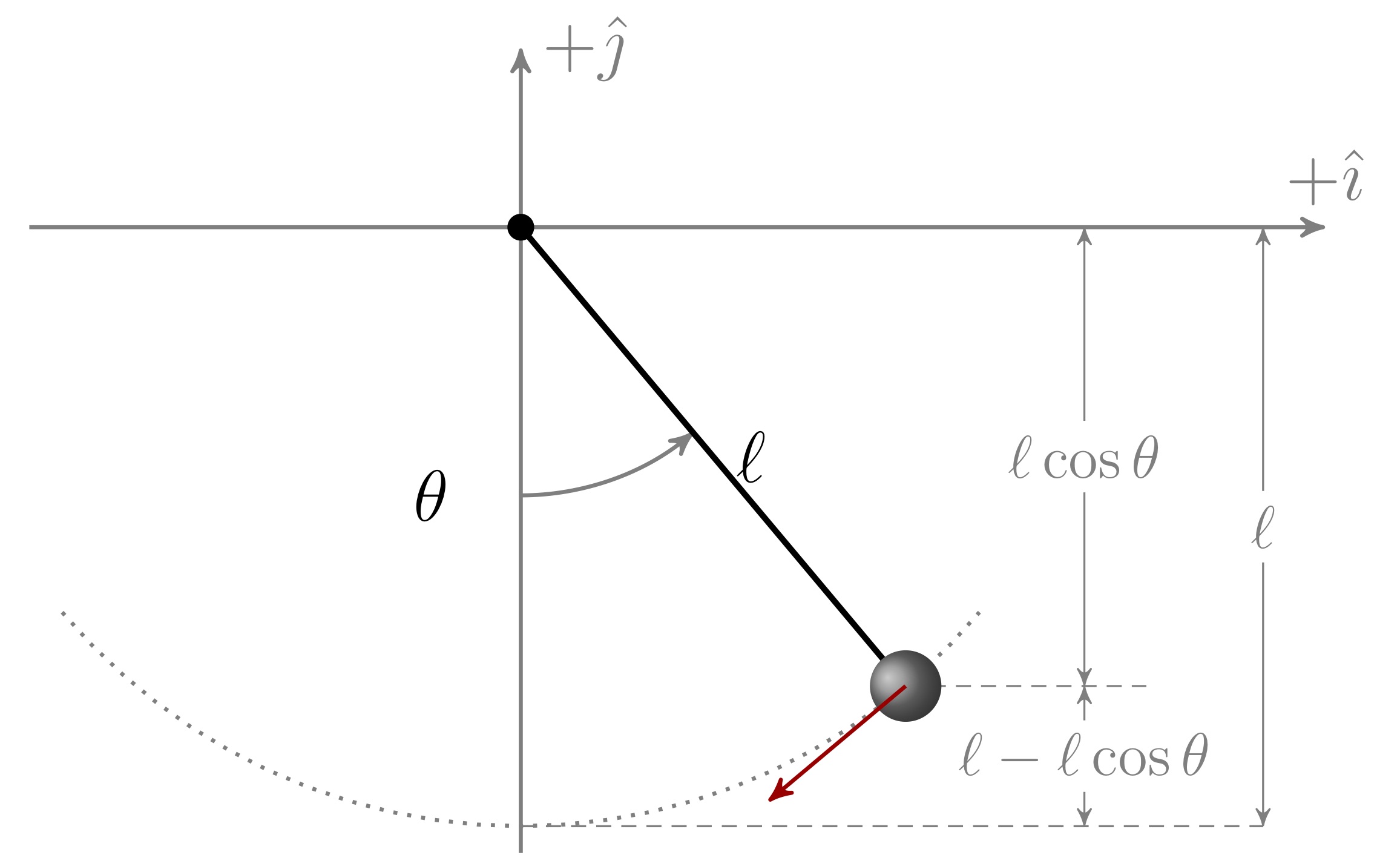
Energía potencial: \[ U_g=mg\ell \left(1-\cos \theta \right) \] Energía cinética: \[ K=\frac{1}{2} m v^2= \frac{1}{2} m (\ell \dot{\theta})^2 \] con \(v=\ell \frac{\mathrm{d}}{\mathrm{d}t}\theta=\ell \dot{\theta} \).
La energía total del péndulo es: \begin{align*} U_g+K &= E \\ mg\ell \left(1-\cos \theta \right) + \frac{1}{2} m (\ell \dot{\theta})^2 &=E \end{align*} La energía se conserva, así que \(E\) es una constante y su derivada debe de ser igual a cero: \begin{align*} \frac{\mathrm{d}}{\mathrm{d}t} E &= 0 \\ \frac{\mathrm{d}}{\mathrm{d}t} \left[ mg\ell \left(1-\cos \theta \right) \right]+ \frac{\mathrm{d}}{\mathrm{d}t} \left[ \frac{1}{2} m (\ell \dot{\theta})^2 \right] &=0 \\ -mg \ell \frac{\mathrm{d}}{\mathrm{d}t} \cos \theta + \frac{1}{2} m \ell^2 \frac{\mathrm{d}}{\mathrm{d}t} \dot{\theta}^2 &=0 \\ mg\ell \sin \theta \dot{\theta} + m \ell^2 \dot{\theta} \ddot{\theta} &= 0 \\ g \sin \theta + \ell \ddot{\theta} &= 0 \end{align*} Por consiguiente la ecuación de movimiento que se obtiene es: \[ \ddot{\theta} = -\frac{g}{\ell} \sin \theta \] En el límite de oscilaciones pequeñas \[ \lim_{\theta\to 0}(\sin \theta)=\theta \] se tiene la ecuación diferencial del oscilador armónico simple \[ \ddot{\theta} = -\frac{g}{\ell} \theta \]
Regresa al inicioLa ley de la gravitación universal de Newton
Observaciones:
- Los cuerpos ejercen una fuerza de atracción sobre otros cuerpos.
- La fuerza de atracción gravitacional es proporcional a las masas involucradas e inversamente proporcional al cuadrado de la distancia que las separa: \begin{equation} F=G\frac{m_1 m_2}{d^2} \end{equation}
- \(F\) módulo de la fuerza ejercida sobre cada una de las masas \(m_1\) y \(m_2\)
- \(d\) distancia de separación entre los centros de masa de los cuerpos \(m_1\) y \(m_2\).
- La fuerza de atracción gravitacional va siempre dirigida a lo largo de la línea que une a los centros de masa de los objetos involucrados: \[ \vec{F}_{12}=-G\frac{m_1 m_2}{\left| \vec{r}_{12}\right|^2}\cdot \frac{\vec{r}_{12}}{\left| \vec{r}_{12}\right|}=-G\frac{m_1 m_2}{\left| \vec{r}_{12}\right|^2}\hat{r}_{12} \]
La fuerza de atracción gravitacional ejercida sobre una masa \(m_2\) debido a la presencia de una masa \(m_1\) es directamente proporcional al producto de las masas, inversamente proporcional al cuadrado de \(\left|\vec{r}_{12}\right|\) la distancia de separación entre los centros de masa y apunta siempre en la dirección de la línea que une a dos centros de masa \(\hat{r}_{12}\): \begin{equation} \vec{F}_{12}=-G\frac{m_1 m_2}{\left| \vec{r}_{12}\right|^2}\hat{r}_{12} \end{equation}
Notese que \(\vec{F}_{12}\) es la fuerza de atracción ejercida por la masa \(m_1\) sobre la masa \(m_2\). Esto se puede ver como si colocáramos a nuestro sistema de referencia en la posición de la masa \(m_1\) y en consecuencia tenemos una fuerza que apunta siempre en la dirección del origen de dicho sistema de referencia y por lo tanto en la fórmula de la fuerza aparece un signo negativo.
El parámetro \(G\) es la constante de la gravitación universal y corresponde a una constante universal. \[ G=6.67384(80)\times 10^{-11} \mathrm{m^3 Kg^{-1}s^{-2}} \]
La descripción moderna de la gravitación nos dice que la fuerza de gravedad se debe a la modificación de la curvatura generada sobre el espacio-tiempo a causa de la existencia de la masa.
Regresa al inicioPrincipio de superposición
\begin{equation} \vec{F}_{k}=\sum_{i=1}^{N}-G\frac{m_i m_k}{\left| \vec{r}_{ik}\right|^2}\hat{r}_{ik} \end{equation}
Regresa al inicioProblemas de la Ley de Gravitación Universal
- El radio de la tierra es de alrededor de \(6370\ \mathrm{km}\). Un objeto cuya masa es igual a \(20\ \mathrm{kg}\) es elevado a una distancia de \(160\ \mathrm{km}\) de la superficie de la tierra. (a) ¿Cuál es la masa del objeto a esa altura? (b) ¿Cuánto pesa el objeto a dicha altura?
- Un gravímetro de átomos fríos es capaz de detectar la variación de la aceleración de la gravedad que la tierra ejerce sobre los átomos de rubidio cerca de la superficie de la tierra cuando la altura del experimento es cambiada en tan solo un metro. Estime la resolución del aparato considerando que el radio medio de la tierra es de \(6371\ \mathrm{km}\).
Solución: La fuerza que ejerce la tierra sobre un átomo cerca de la superficie de la tierra y a una altura \(\Delta R\) por encima de dicha posición es respectivamente \[ F(R_T)=G\frac{m_{a}\, M_{T}}{R_{T}^2} \hspace{0.5cm} \mathrm{y} \hspace{0.5cm} F(R_T+\Delta R)=G\frac{m_{a}\, M_{T}}{(R_{T}+\Delta R)^2} \] \begin{align*} \frac{\Delta F}{F(R_T)}&=\frac{F(R_T)-F(R_T+\Delta R)}{F(R_T)} =1-\frac{F(R_T+\Delta R)}{F(R_T)} \\ &=1-\left( G\frac{m_{a}\, M_{T}}{(R_{T}+\Delta R)^2}\right)/\left(G\frac{m_{a}\, M_{T}}{R_{T}^2}\right)\\ &=1-\frac{R_T^2}{(R_T+\Delta R)^2}=1-\frac{1}{(1+\Delta R/R_T)^2}\\ &=1-\frac{1}{\left[1+\left( 1\ \mathrm{m} /6371\times 10^3\ \mathrm{m} \right)\right]^2} \approx 3\times 10^{-7} \end{align*} Este resultado indica que nuestro aparato de medición tiene que ser capaz de distinguir al menos tres partes en diez millones. Esto implica que cada Newton de fuerza que registra este aparato lo puede determinar con una barra de incertidumbre de aproximadamente \(0.0000003\ \mathrm{N}\) y la lectura correspondiente la reportaríamos como \(1.0000000(3)\ \mathrm{N}\).
El potencial gravitacional
De la definición de la energía potencial, \[ W=-\Delta U \] vamos a encontrar el valor de la energía potencial del campo gravitacional calculando el trabajo realizado para traer a un objeto \(m\) cerca de otro objeto \(M\).
Observemos que la definición anterior únicamente indica un cambio en la energía. Por tal motivo tenemos que definir el cero de la energía potencial y resulta natural pensar que cuando los dos objetos se encuentran infinitamente lejos el uno del otro, la energía potencial asociada a esa situación debe de ser cero. Entonces, \[ \Delta U=-\int_{\infty}^{r'} \vec{F}\cdot d\vec{r} \] Ahora recordemos que la fuerza gravitacional es siempre paralela al vector que une a los dos objetos interactuantes, por lo que podemos realizar la integral usando únicamente las magnitudes de los vectores \begin{align*} \Delta U=-\int_{\infty}^{r'} \left( -G\frac{m M}{r^2}\right) dr &= G m M\int_{\infty}^{r'} \frac{1}{r^2} dr \\ &= G m M \left(-\frac{1}{r} \right)\Big|_{\infty}^{r'} \\ &= -G m M \left[ \frac{1}{r'}-\frac{1}{\infty} \right] =-G\frac{m M}{r'} \end{align*} Por lo tanto, podemos definir a la energía potencial asociada a un campo de fuerza gravitacional de la siguiente manera: \[ U_g(r)=-G \left(\frac{m M}{r}\right) \] con \(r=\left(x^2+y^2+z^2\right)^{1/2}\).
\begin{tikzpicture} \begin{axis}[ height=0.38\textwidth, width=0.62\textwidth, xmin=0,xmax=0.5, ymin=-10,ymax=8, grid=major, xlabel=$r$,% ($\metre$), ylabel=$U$,% ($\joule$), %extra x ticks={13.8}, %extra x tick labels={$\mu_e F_N$}, extra x tick style={grid style={dashed,green!50!black},green!50!black,tick pos=right, grid=major, ticklabel pos=right, tick label style={font=\small}}, %extra y ticks={10.8}, %extra y tick labels={$\mu_c F_N$}, extra y tick style={grid style={dashed,red},red,tick pos=right, grid=major, ticklabel pos=right, tick label style={font=\small}} ] %\node at (0.3,0) {}; \node[pin=-40:$U_g$,draw=blue] at (axis cs:0.4,-2.5) {}; \node[pin=45:$U_{rep.}$,draw=green] at (axis cs:0.2,2.65) {}; %\node at (3.75cm,1.9cm) {Cinética}; \addplot[domain=0.0155:0.5,samples=100,blue,thick] {-1/x}; \addplot[domain=0.015:0.5,samples=100,green,thick] {0.5/(x-0.015)}; \addplot[domain=0.015:0.5,samples=200,red,thick] {-1/x+0.5/(x-0.015)}; %\addplot[domain=13.8:25,blue,thick] {10.8+3*exp(-3*(x-13.8))}; %\addplot[domain=6:10,blue] {-5}; %\draw[dotted] (axis cs:13.8,15) -- (axis cs:13.8,-2); %\draw[dotted] (axis cs:-2,10.8) -- (axis cs:28,10.8); %\addplot[soldot] coordinates{(13.8,13.8)}; %\addplot[holdot] coordinates{(4,16)(6,6)(10,-5)}; \end{axis} \end{tikzpicture}Demostremos ahora que este potencial esta asociado a la fuerza gravitacional mediante \(\vec{F}=-\vec{\nabla}U_g\), es decir, vamos a mostrar que la fuerza gravitacional \(\vec{F}\) la podemos expresar como el gradiente del potencial \(U_g\): \begin{align*} \vec{F} &=-\left\lbrace\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z} \right\rbrace U_g \\ &= G m M\left\lbrace\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z} \right\rbrace \left(\frac{1}{r} \right) \\ &= G M m (-r^{-2})\frac{1}{2}\left[x^2+y^2+z^2\right]^{-1/2} \left\lbrace 2x,2y,2z \right\rbrace \\ &= -GMm (r^{-2})\frac{1}{2}(r^{-1}) \left\lbrace 2x,2y,2z \right\rbrace \\ &= -GMm\frac{\left\lbrace x,y,z \right\rbrace}{\left|\vec{r}\right|^{3}}=-G\frac{M m}{r^2} \hat{r} \end{align*} \[ \hspace{-1cm} \therefore \hspace{1cm} \vec{F}=-G\frac{M m}{r^2} \hat{r} \]
Regresa al inicioMensajes
Otros
- Videos del profesor Walter Lewin en el MIT:
- Harvard Natural Sciences Lecture Demonstrations: